How To Find Increasing And Decreasing Intervals On A Graph Calculus
If our first derivative is positive, our original function is increasing and if g'(x) is negative, g(x) is decreasing. Giving you the instantaneous rate of change at any given point.

Algebra 2 Word Wall (With images) Algebra, Word wall
The graph will help you visualize it better.

How to find increasing and decreasing intervals on a graph calculus. A x 2 + b x + c = a ( x + b 2 a) 2 + c − b 2 4 a. So once you find out the function is increasing in the open interval ( a, b) by using differentiation criteria, then you can manually check that the conditions apply to the endpoints by showing that. Then set f' (x) = 0.
For this particular function, use the power rule: Find intervals of increasing, decreasing, and intervals of concavity up, down and point of inflection (s), use calculus to find these values exactly (if possible): Since f ' (x) > 0, therefore the function is increasing at this interval.
Consider f0(x) = 2x−5 f0(x) > 0 if x > 5/2, f0(x) < 0 if x < 5/2. So your goal is to find the intervals of increasing and decreasing, which essentially means you're trying to find where the instantaneous slopes are increasing or decreasing, which is the definition of a derivative: If the value is positive,then that interval is increasing.
{eq}\displaystyle y = \dfrac {x. Now, let us take a point from the interval. To find increasing and decreasing intervals, we need to find where our first derivative is greater than or less than zero.
If f′(x) > 0 at each point in an interval i, then the function is said to be increasing on i. The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. Fun‑4 (eu), fun‑4.a (lo), fun‑4.a.1 (ek) google classroom facebook twitter.
So, find by decreasing each exponent by one and multiplying by the original number. To see this formula is true, just multiply out. Attach is an image that may help you:
As someone mentioned in the comments, the standard way to do this is the trick of completing the square (also often used to derive the quadratic formula). So we're looking for a cz. If the value is negative, then thatinterval is decreasing.
So to find intervals of a function that are either decreasing or increasing, take the derivative and plug in a few values. The graph is increasing until x=1.5, then decreases. Then solve for any points where the derivative equals 0.
Find where f(x) = x2 − 5x + 1 is increasing and where it is decreasing. And the function is decreasing on any interval in which the derivative is negative. That is, find all \(c\) in \(i\) where \(f'(c) = 0\) or \(f'\) is not defined.
Because the derivative is zero or does not exist only at critical points of the function, it must be. Find the critical values (solve for f ' (x) = 0) thesegive us our intervals. Next, we can find and and see if they are positive or negative.
Procedure to find where the function is increasing or decreasing : F′(x) < 0 at each point in an interval i, then the function is said to be decreasing on i. Let's try a few of these:
How do we determine the intervals? Since f ' (x) < 0, hence the function is decreasing at this interval. Now, choose a value that lies in each of theseintervals, and plug them into the derivative.
So here in blues are function f of x and we are to find an open interval where f of x is for part a increasing and for part b decrease just by looking at the graph. Find the critical values of \(f\). Lim x → a + f ( x) ≥ f ( a) and lim x → b − f ( x) ≤ f ( b)
Finding increasing interval given the derivative. The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. F0(x) > 0(f0(x) < 0) ⇒ is increasing (decreasing) example 3.
Put solutions on the number line. To find intervals on which \(f\) is increasing and decreasing: To find the an increasing or decreasing interval, we need to find out if the first derivative is positive or negative on the given interval.
Figure 3 shows examples of increasing and decreasing intervals on a function. So let's start with a so we know that a function is increasing when the graph goes up from left to right. F ( x) = x 3 − 1 2 x.
Finding decreasing interval given the function. The first step is to take the derivative of the function. Choose random value from the interval and check them in the first derivative.
We can say this because its only a parabola. If f (x) > 0, then the function is increasing in that particular interval. Determining intervals on which a function is increasing or decreasing.
Finding intervals of increase and decrease of a function can be done using either a graph of the function or its derivative.these intervals of increase and decrease are important in finding critical points, and are also a key part of defining relative maxima and minima and inflection points. For this exact reason we can say that there's an absolute max at f(1). So this problem, we're given the graph of f of x.
A function is considered increasing on an interval whenever the derivative is positive over that interval.

Increasing and Decreasing Functions Activity Algebra

Interval notation Intervals, Homework help, Notations

Exponential Functions Quick Check and WarmUp Template

Height of Waist Off Ground linear, piecewise, increasing

Algebra Word Wall Math word walls, Algebra, Algebraic

Decreasing Number Line Sequences with Missing Numbers (Max

Exponential Functions Quick Check and WarmUp Template in

Piecewise, Absolute Value and Step Functions
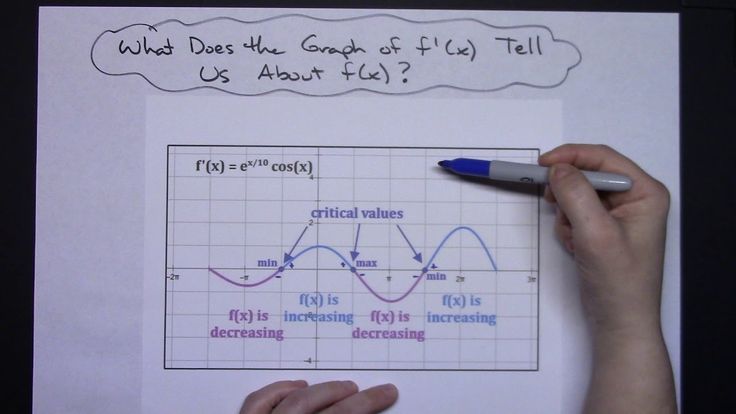
Analyzing the Graph of the Derivative Calculus

Digital Piecewise Functions Drag and Drop Activity for

Finding Increasing & Decreasing Intervals and Max/Min

Graphing Polynomials {cheat sheet!} High school algebra

Google Drive BUNDLE POLYNOMIAL FUNCTIONS Distance

Name That Function Characteristics of Graphs Math

Introduction to increasing, decreasing, positive or




Post a Comment for "How To Find Increasing And Decreasing Intervals On A Graph Calculus"